La scodella di Galileo è appunto una figura geometrica che assomiglia a una scodella. Vediamo come viene descritta la sua costruzione da Salviati:
È necessario farne la figura, perché la prova è pura geometrica. Per tanto intendasi il mezzo cerchio AFB, il cui centro C, ed intorno ad esso il parallellogrammo rettangolo ADEB, e dal centro a i punti D, E siano tirate le rette linee CD, CE; figurandoci poi il semidiametro CF, perpendicolare a una delle due AB, DE, immobile, intendiamo intorno a quello girarsi tutta questa figura: è manifesto che dal rettangolo ADEB verrà descritto un cilindro, dal semicircolo AFB una mezza sfera, e dal triangolo CDE un cono. Inteso questo, voglio che ci immaginiamo esser levato via l'emisferio, lasciando però il cono e quello che rimarrà del cilindro, il quale, dalla figura che riterrà simile a una scodella, chiameremo pure scodella.
Per visualizzare bene la figura in tre dimensioni:
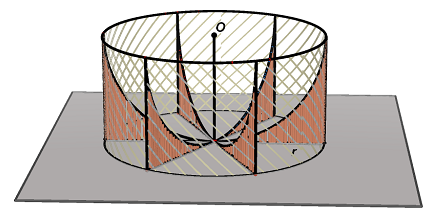
Si dimostra prima l'equivalenza tra cono e scodella; poi tracciando un piano parallelo alla base della scodella, si può dimostrare l'equivalenza superficiale tra il cerchio di diametro HL e la corona circolare individuata dalle circonferenze di centro P e raggi PG e PI.
Per visualizzare bene la circonferenza e la corona circolare:
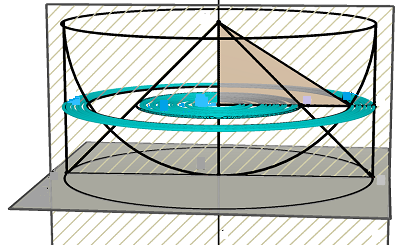
La figura descritta da Salviati è la seguente:
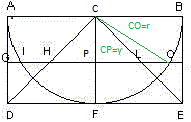
Dato il raggio della sfera uguale a r (esso conicide anche con l'altezza del cilindro); il volume della scodella sarà dato da :
Volume del cilindro = πr2h = 2πr3
| Volume semisfera = | 2 3 | πr3 |
|---|
| Volume scodella = Volume cilindro - Volume semisfera = πr3- | 2 3 | πr3 = | πr3 3 |
|---|
| Volume Cono = | πr2h 3 | = | πr3 3 |
|---|
Andiamo ora a vedere l'equivalenza tra le due superfici sopra citate. Chiamando PC = y e sapendo che CO = r calcoliamo la lunghezza del segmento PO, allora per il teorema di Pitagora:
PI = PO = √(CO2-PC2) = √(r2-y2)
Area corona circolare = πr2 - π[√(r2 - y2)]2 = πy2
Area circorferenza di diametro HL = πy2